Back at it again with some new resources. I’m learning Big O Time Notation again but with some lectures notes from MIT and a whole lot of diagrams and googling. So I was reading the “Cracking the Coding Interview” book and it emphasized being comfortable using Big O Notation on Algorithms problems. I thought I should take that to heart and produce clear notes that answer my own questions on the subject. This endeavor has taken me down memory lane. I revisited the concept of limits and asymptotes in mathematics to start. I’m trying not to rush with this and to make sure I understand everything I cover on the topic.
TLDR;
Okay, so here are the highlights of what I did:
- Read through the Big O notation section in “Cracking the Coding Interview” by Gayle L. McDowell. It outlined some of the basic algorithms and their corresponding Big O notation formulas. Right off the bat I found mistakes I had been making. I have covered big O notation in the past but I clearly have a lot of room to improve.
- I ended up finding a resource on
x86_64assembly language code. I kept a bookmark for it but I will stick to Big O notation for now. I feel like I might be jumping around too much. There is a method to all this madness but it’s a process for me. I think Big O notation and algorithm / data structures work takes a priority over assembly at this point. I really want to better understand how tools like Git were built.
Notes on Big O Notation
This is an extremely important concept. Big O time is the language and metric we use to describe the efficiency of algorithms. Not understanding it thoroughly can really hurt you in developing an algorithm. Not only might you be judged harshly for not really understanding big O, but you will also struggle to judge when your algorithm is getting faster or slower.
The goal of these notes is to help me better understand this concept and identify the correct big O equations for all the algorithms I see.
Asymptotic runtime (big O time)
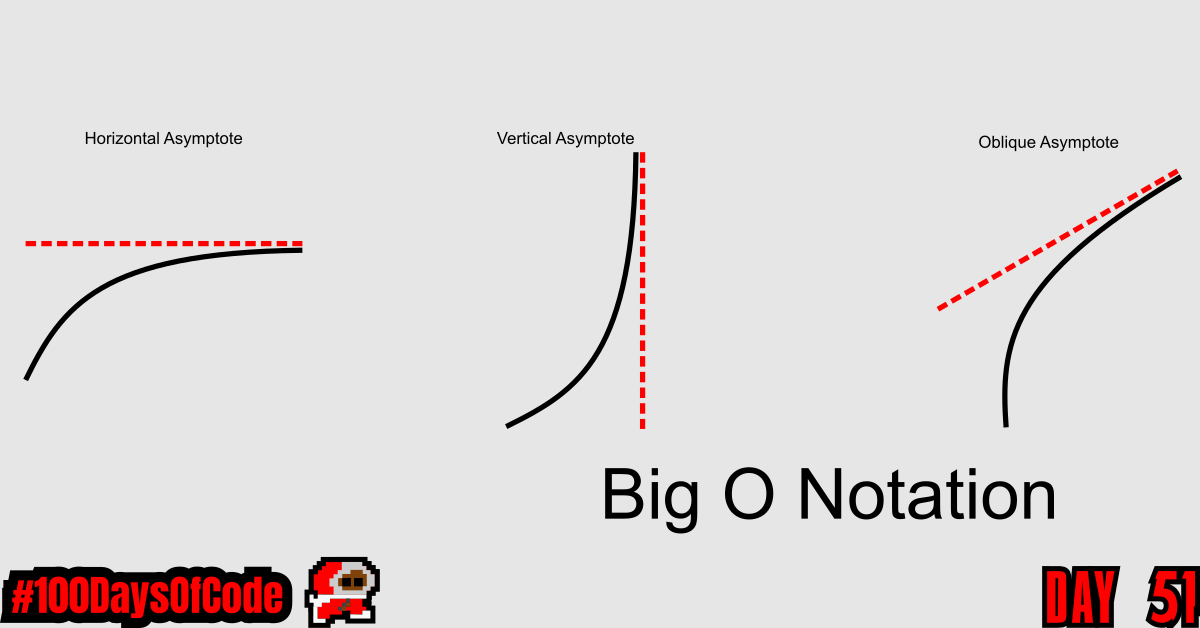
Asymptotic is the adjective form of the word Asymptote. An asymptote is a line that a curve approaches, as it heads towards infinity. They are usually involved when calculating limits in mathematics. We can also utilize them when measuring the efficiency of algorithms (a.k.a. Big O notation).
In mathematical analysis, asymptotic analysis (Asymptotics) is a method of describing limiting behavior.
As an illustration, suppose that we are interested in the properties of a function f(n) as n becomes very large. If f(n) = n^2 + 3n, the n as n becomes very large, the term 3n becomes insignificant compared to n^2. The function f(n) is said to be “asymptotically equivalent to n^2 , as n → infinity “. This is often written symbolically as f(n) ~ n2, which is read as f(n) is asymptotic to n2.
References
Conclusion
That’s all for today. If you are interested in the MIT course you can check out the video lecture I’m currently going through. The lecture is helpful but isn’t sufficient by itself. Anyways, until next time PEACE!