Got through some MIT notes on Big O notation and some of the math behind it. I am not the best at the theories and history behind most of the math I use but I tried with this one. I wrote and re-wrote my notes over and over to try and make the information my own. I will probably need to revisit this topic later but for now I can move onto some example problems.

TLDR;

Okay, so here are the highlights of what I did:

• Read through the Big O notation section in “Cracking the Coding Interview” by Gayle L. McDowell. I started focusing on the example problems and writing good notes breaking down each one.
• Finished notes on the MIT Big O Notation lecture. I am still a little fuzzy on the topic but I think I somewhat understand the math. I am hoping a bit of time and review will help all of this sink in.

Notes on Big O Notation

What is Big O Time Notation?

Big O Time Notation or “Big O” for short, is a system used to consistently represent the efficiency of functions / procedures / algorithms. Software developers by virtue, want to use the most efficient algorithms possible. By using Big O, we can quickly calculate and compare functions / procedures / algorithms to determine which are the most efficient. Big O has some rules that must be upheld:

• When performing any calculation
• When writing any formula

These rules are derived from math and are what make Big O so useful at providing comparable values for efficiency. I do not have the best grasp of these rules but I will try to explain them later down in these notes.

What Affects the Efficiency of a Computer Program?

When thinking about a computer’s efficiency, we must recognize that it involves more than just one thing. It involves the computer’s:

• CPU (time) usage
• Memory usage (short term temporary memory???)
• Disk usage (long term permanent memory???)
• Network usage
• Maybe a few more bells and whistles I am unaware of ???

When we write code, we must keep all of these factors in mind. Depending on the programs that we run, we will use more or less of these resources. This is referred to as the performance of the program (Some programs are a lot more taxing on the computer due to the nature of the tasks that they perform).

The performance of a program can be influenced by the hardware on the computer, the compiler, and most importantly, the code from the program itself (a.k.a. the developer’s work). If we write overly complex code we can decrease the performance of the program which would tax the computer more than it needs to. In contrast to this, sleek code can streamline the program and improve it’s performance.

Big O Notation focuses on this complexity in our code and how it effects the performance of a program.

How do Operations in a Computer Program affect Complexity????

The time required by a function/procedure is proportional to the number of “basic operations” that it performs. Here are some examples of basic operations:

• One arithmetic operation (e.g. addition, subtraction, multiplication, division, etc)
• One assignment (e.g. let x = 10)
• One test (e.g. x == true)
• One read (of a primitive type: integer, float, character, boolean)
• One write (of a primitive type: integer, float, character, boolean)

However, not all functions/procedures are the same. In the context of efficiency, Big O, and code complexity, we have two types that we must be aware of:

• “Constant Time” functions/procedures (They always perform the same number of operations and take the same amount of time to perform them)
• “Variable Time” functions/procedures (The number of operations they perform and the time they take to perform them changes based on the Problem/Input Size)

The Problem Size / Input Size is represented in many different ways. However, we generally can see them as:

• The size of an array
• The number of list items
• The number of characters in a string
• etc.

As the Problem/Input Size changes for a “Variable Time” function/procedure so does it’s efficiency. Representing the rate of change in efficiency of said function/procedure is what we use Big O Notation for. Using Big O notation we can hopefully compare solutions to find the ones have a high efficiency when the Problem/Input Size is small while maintaining a relatively low rate of change in efficiency as the Problem/Input Size increases.

When we are trying to find the complexity of the function/ procedure/ algorithm/ program, we are not interested in the exact number of operations that are being performed. Instead, we are interested in the relation of the number of operations to the problem size.

Typically, we are usually interested in the worst case: what is the maximum number of operations that might be performed for a given problem size. For example, inserting an element into an array, we have to move the current element and all of the elements that come after it one place to the right in the array. In the worst case, inserting at the beginning of the array, all of the elements in the array must be moved. Therefore, in the worst case, the time for insertion is proportional to the number of elements in the array, and we say that the worst-case time for the insertion operation is linear in the number of elements in the array. For a linear-time algorithm, if the problem size doubles, the number of operations also doubles.

How is Big O Calculated with Math

In mathematics the formal definition of a Big O expression would be:

A function T(N) is O( F(N) ) if for some constant c and for values of N greater than some value n subscript 0:

T(N) <= c * F(N)

now… currently, I do not know what n subscript 0 means but I will try to figure it out later

• T(N) = the exact complexity of a procedure/function/algorithm as a function of the problem size N
• F(N) = is an upper-bound (Max value) on the complexity of T(N) (i.e., the actual time/space complexity for a problem of size N will be no worse than F(N)).
• c is a constant that supports the definition in each particular Big O expression. It is not some set value (I think…).
• n subscript 0 is the value of N that is so small that the Big O expression does not accurately apply. (I think…). I mean Big O is intended to focusing on the scaling and large N values. Not super small values.

Just to provide a bit more clarity… T(N) is implying that the complexity of the procedure/function/algorithm called T is the result of a set of operations being applied to a variable N (which we know N to be the varying problem/input size). The complexity of the procedure/function/algorithm is T(N). With the worst case scenario being represented by F(N).

In practice, we want the smallest F(N) — the least upper bound on the actual complexity. For example, consider:

T(N) = 3 * N^2 + 5.

We can show that T(N) is O(N^2) by choosing c = 4 and n subscript 0 = 2.

This is because for all values of N > 2 :

( 3 * N^2 + 5 ) <= ( 4 * N^2 )

if N = 3:

T(N) = 3 * (3^2) + 5 = 32

c * F(N) = 4 * (3^2) = 36

T(N) is not O(N), because whatever constant c and value n subscript 0 you choose, There is always a value of N > n subscript 0 such that (3 * N^2 + 5) > (c * N)

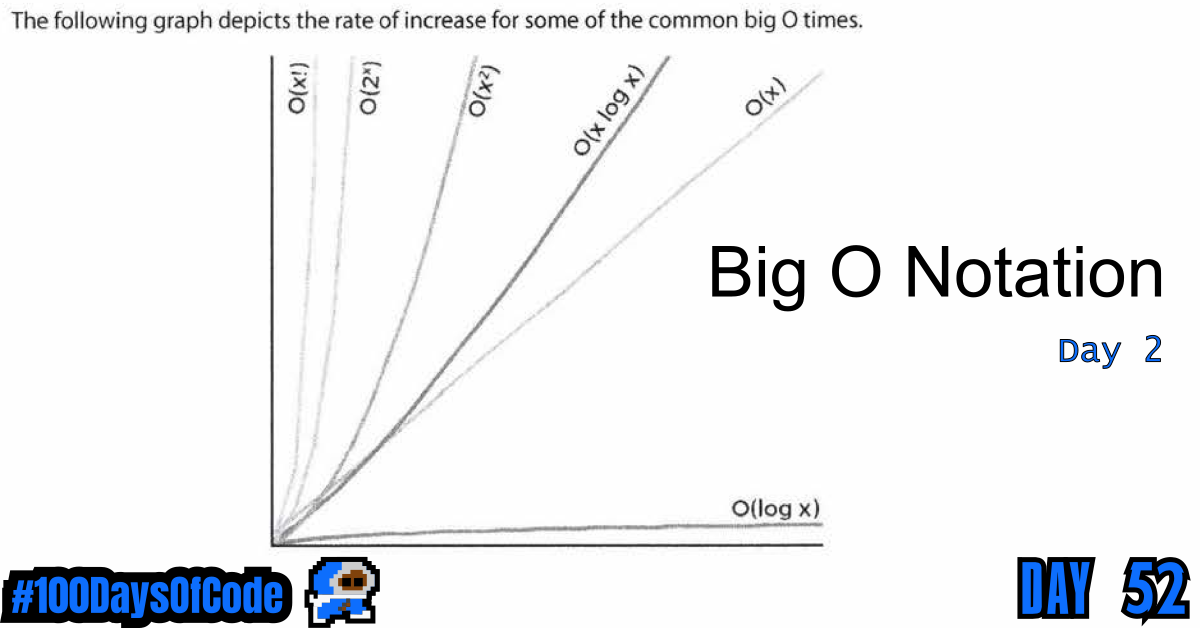
Classes of Functions in Big O Notation

Here is a list of the different types of functions represented in Big O notation. The list is organized in the order of slowest growing to the fastest growing.

Notation        Name
--------        ---------
O(1)            Constant
O(log(n))       Logarithmic
O((log(n))^c)   Polylogarithmic
O(n)            Linear
O(n^2)          Quadratic
O(n^c)          Polynomial
O(c^n)          Exponential

• The slowest growing algorithms are the least complex and the most efficient in their use of space/time

How to Determine Complexities for Big O Notation

In general, how can you determine the running time of a piece of code? The answer is that it depends on what kinds of statements are used.

Sequence of statements

statement 1;
statement 2;
...
statement k;

The total time is found by adding the times for all statements:

total time = time(statement 1) + time(statement 2) + ... + time(statement k)

If each statement is “simple” (only involves basic operations) then the time for each statement is constant and the total time is also constant: O(1).

If-Then-Else

if (cond) then
  block 1 (sequence of statements)
else
  block 2 (sequence of statements)
end if;

Here, either block 1 will execute, or block 2 will execute. Therefore, the worst-case time is the slower of the two possibilities:

max( time(block 1), time(block 2) )

If block 1 takes O(1) and block 2 takes O(N), the if-then-else statement would be O(N).

Loops

for i in 1 .. N loop
  sequence of statements
end loop;

The loop executes N times, so the sequence of statements also executes N times. If we assume the statements are O(1), the total time for the for loop is N * O(1), which is O(N) overall.

Nested loops

for i in 1 .. N loop
  for j in 1 .. M loop
    sequence of statements
  end loop;
end loop;

The outer loop executes N times. Every time the outer loop executes, the inner loop executes M times. As a result, the statements in the inner loop execute a total of N * M times. Thus, the complexity is O(N * M).

In a common special case where the stopping condition of the inner loop is J < N instead of J < M (i.e., the inner loop also executes N times), the total complexity for the two loops is O(N^2).

Statements with function/ procedure calls

When a statement involves a function/ procedure call, the complexity of the statement includes the complexity of the function/ procedure. Assume that you know that function/ procedure f takes constant time (O(1)), and that function/procedure g takes time proportional to (linear in) the value of its parameter k. Then the statements below have the time complexities indicated.

f(k) has O(1)
g(k) has O(k)

When a loop is involved, the same rule applies. For example:

for J in 1 .. N loop
  g(J);
end loop;

has complexity (N^2). The loop executes N times and each function/procedure call g(N) is complexity O(N).

Conclusion

That’s all for today. If you are interested in the MIT course you can check out the video lecture I’m currently going through. The lecture is helpful but isn’t sufficient by itself. Anyways, until next time PEACE!